Küre nedir ve nasıl oluşur? Yarıçap ve çap neyi ifade eder? Kürenin yüzey alanı ve hacmi nasıl hesaplanır? Doğada ve mühendislikte kürenin önemi nedir? Tüm detaylar için okumaya devam edin!
Küre, geometri dünyasında özel bir yer tutan hacimli bir şekildir. Tüm yüzey noktalarının, kürenin merkez noktası olarak adlandırılan sabit bir noktadan eşit uzaklıkta olduğu bir cisimdir. En temel haliyle bir top veya zıpzıp, kürenin günlük yaşamda karşımıza çıkan örneklerindendir. Bu şeklin simetrik yapısı, hem matematikte hem de doğada birçok uygulama alanı bulmasına neden olur.
Kürenin oluşturulması, iki farklı yöntemle kavramsallaştırılabilir:
- Merkez adı verilen bir noktadan eşit uzaklıktaki noktaların bir araya getirilmesiyle bir küre meydana gelir. Bu, geometride kürenin temel tanımıdır.
- Bir dairenin herhangi bir çapı etrafında 360° döndürülmesiyle küre oluşturulur. Bu yöntem, kürenin hacimsel ve simetrik yapısını anlamayı kolaylaştırır.
Kürenin Temel Kavramları
Küreyi anlamak için bazı temel terimlerin bilinmesi gerekir:
- Merkez: Kürenin sabit noktasını ifade eder. Tüm yüzey noktaları bu noktadan eşit uzaklıktadır.
- Yarıçap (r): Kürenin yüzeyindeki bir noktayı, merkeze bağlayan doğru parçasına yarıçap denir. Yarıçap, kürenin temel ölçüsüdür ve çoğu matematiksel işlemde bu büyüklük kullanılır.
- Çap (d): Kürenin yüzeyi üzerindeki bir noktadan geçerek merkeze ulaşan ve karşı tarafa uzanan doğru parçasıdır. Çap, iki yarıçap uzunluğuna eşittir ve d = 2r formülüyle ifade edilir.
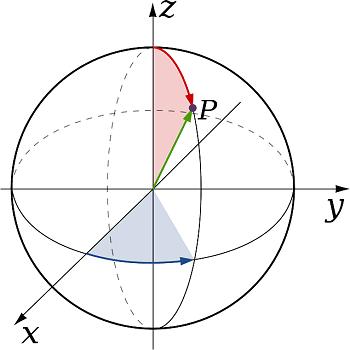
Kürenin Matematiksel Özellikleri
Kürenin Alanı
Bir kürenin yüzey alanı, şu formül ile hesaplanır:

Bu formüle göre, kürenin yüzey alanı, yarıçapının karesine bağlıdır. Yani yarıçap iki katına çıktığında, yüzey alanı dört katına çıkar. Örneğin, yarıçapı 1 birim olan bir kürenin yüzey alanı yaklaşık 12,57 birim² iken, yarıçap 2 birime çıktığında yüzey alanı 50,27 birim² olur.
Kürenin Hacmi
Kürenin içerdiği hacim, aşağıdaki formül ile hesaplanır:

Kürenin hacmi, yarıçapının küpüyle doğru orantılıdır. Örneğin:
- Yarıçapı 1 birim olan bir kürenin hacmi yaklaşık 4,19 birim³ olur.
- Yarıçap 2 birime çıktığında, hacim 33,51 birim³’e yükselir.
Bu, kürenin boyutları büyüdükçe hacminin çok hızlı bir şekilde arttığını gösterir.
Kürenin Matematik ve Geometrideki Yeri
Küre, matematiğin ve fiziğin birçok alanında temel bir figürdür. Özellikle geometri, analitik matematik ve diferansiyel denklemlerde sıkça karşımıza çıkar. Ayrıca küre, doğadaki birçok şeklin temel birimi olarak kabul edilir. Gezegenler, yıldızlar ve su damlaları, bu mükemmel simetrik şekle örnek olarak verilebilir.
Kürenin Doğadaki Uygulamaları
Küre, doğada birçok yerde karşımıza çıkar:
- Gezegenler ve yıldızlar: Yerçekimi kuvveti, büyük cisimleri küresel hale getirir. Örneğin, Dünya neredeyse mükemmel bir küredir.
- Su damlaları: Yüzey gerilimi, su damlalarını küresel hale getirir. Küre şekli, en az yüzey alanıyla maksimum hacmi barındırır.
- Atom yapıları: Atomların çekirdekleri ve elektronların dağılımı genellikle küresel bir düzen gösterir.
Küre ve Mühendislik
Kürenin mühendislikteki önemi büyüktür. Özellikle aerodinamik tasarımlarda ve topolojide küresel şekiller sıkça kullanılır. Örneğin:
- Uydular, küresel yapıları sayesinde eşit yüzey dağılımı sağlar.
- Futbol topları, küresel şekilleri sayesinde düzgün bir şekilde yuvarlanır ve aerodinamik davranış sergiler.
Kürenin Günlük Hayattaki Yeri
Küre şekli, yaşamımızda birçok pratik uygulama alanı bulur.
- Spor: Futbol, basketbol ve tenis gibi birçok spor dalında kullanılan toplar küreseldir. Bu, topun düzgün yuvarlanmasını ve hareket etmesini sağlar.
- Dekorasyon: Küresel lambalar ve süs eşyaları, estetik bir görünüm sunar.
- Bilimsel araçlar: Küresel teleskop kubbeleri, ışığın homojen bir şekilde dağılmasını sağlar.
Kürenin Tarihçesi
Küre, antik çağlardan beri matematikçilerin ve filozofların ilgisini çekmiştir. Örneğin:
- Eski Yunan Matematiği: Pisagor ve Arşimet gibi matematikçiler, kürenin geometrik özelliklerini incelemiştir.
- Rönesans Dönemi: Sanatçılar, perspektif ve hacim hesaplamalarında küreyi sıkça kullanmıştır.
Küre ile İlgili İleri Düzey Matematik
Kürenin sadece temel alan ve hacim hesaplamaları değil, aynı zamanda daha karmaşık matematiksel özellikleri de incelenir:
- Küre üzerinde diferansiyel geometri: Kürenin eğrilik özellikleri hesaplanır.
- Analitik matematik: Küre denklemleri ve koordinat sistemleri geliştirilir.
- Küre integralleri: Üç boyutlu uzayda yüzey ve hacim integralleri küre üzerinde uygulanır.
Sonuç
Küre, hem geometrik bir şekil hem de matematiksel bir kavram olarak evrenin her alanında karşımıza çıkar. Yüzey alanı ve hacim hesaplamalarındaki basit formüllerle günlük hayatta kolayca kullanılabilir. Aynı zamanda, doğada ve mühendislikte eşsiz bir yer tutar. Küreyi anlamak, hem matematiksel düşünme yeteneğini hem de çevremizi anlama kapasitemizi artırır.


